
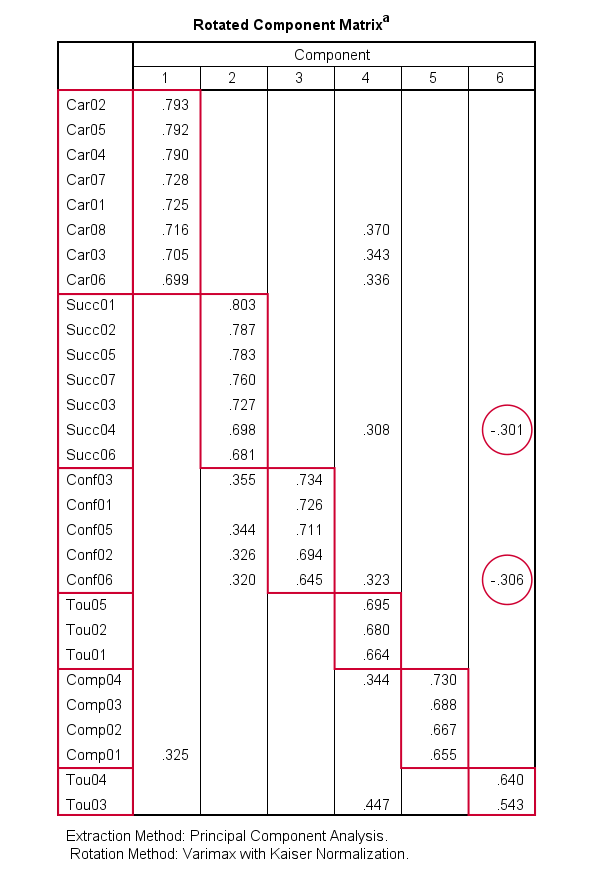
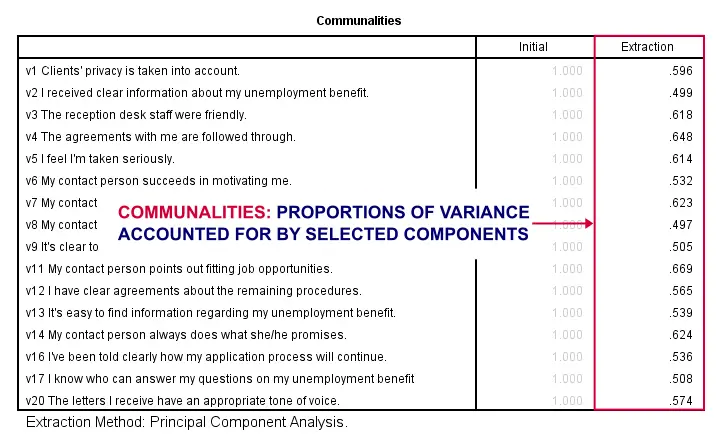
Coefficients of that linear combination are the pattern matrix values. It the model, the being predicted variable is meant either standardized (in a FA of correlations) or centered (in a FA of covariances) observed feature, while the factors are meant standardized (with variance 1) latent features. $^1$ Pattern loadings are the regression coefficients of the factor model equation. Variable loaded by it is its mask: factor in it shows through what appears to be completely not that factor in it. Factor is thin and sleek, it is not like pangolin or armful of whatever. If you do not perceive a construct as univariate trait then using classic factor analysis would be questioned. Also factor scores coefficient matrix is what is useful in addition to pattern and structure loadings in the job of selection items for a factor construct. the item is loaded by the factor - and desirably only by this one - which scale we're constructing). 40), select the item if its situation in pattern matrix confirms the decision (i.e. Usually I include an item in a scale this way: (1) look at maximal correlation (structure matrix) in the item's row (2) if the value is above a threshold (say. Just remember that in psychometry common validity coefficient is correlation (and not regression) coefficient between construct/criterion and item. And it can rise when we validate items in questionnaire construction, - that is, decide which variables to select and which to drop in the scale being created. Structure matrix seems to me potentially better than pattern matrix in back interpretation of variables by factors, if such a task arises. For pilot study and tentative interpretation structure matrix might be better choice. Relying on pattern matrix in interpretation requires well planned study with sufficient sample size. Weak side of pattern matrix is that it is less stable from sample to sample (as usually regression coefficients in comparison to correlation coefficients). The latter case will mean that it is that part of X which is different from Y what loads V so much and thence the V-X pattern coefficient is what is highly valuable in interpretation of X. While V ought to correlate higher and higher with both factors, the regression coefficients can rise both or only one of the two. The more two factors X and Y correlate with each other the greater can be the discrepancy between the pattern loadings and the structure loadings on some variable V. Structure matrix contains (zero-order) correlations between factors and variables. Because it is regression coefficients $^1$. Coefficients of pattern matrix are the unique loads or investments of the given factor into variables. If it is this the strategy typically preferred then pattern matrix appears to be the main tool for interpretation. Correlatedness thus gets to be an isolated characteristic of entities from the labels of the entities. That is, ideally, factor X label would dissociate from a correlated factor Y label, to stress individuality of both factors, while assuming that "in outer reality" they correlate. With oblique rotation, factors are not orthogonal still, we usually prefer to interpret a factor as clean entity from the other factors.
Since factor is univariate essence it should be interpreted as the (relatively simple) meaning lying on (or "behind") the intersection of the meanings/contents of the variables loaded by the factor. Term "construct" in psychometry is generic and could be conceptualized as factor (essence) or cluster (prototype) or something else. It is not the same thing as a set or cluster of phenomena. Theoretically, factor of Factor analysis is a univariate latent feature, or essence. It is about rotations and can hint towards or partly answer your question.Ī more specific answer from me about interpretation might be as follows.
PSPP can work with SPSS data files and has a comparable syntax. It does not limit the number of cases or variables which can be used and can be interacted with via a graphical or terminal user interface. GNU PSPP is a program for statistical analysis of sampled data and a free alternative to SPSS.


 0 kommentar(er)
0 kommentar(er)
